The “3DES-HMAC” challenge
This challenge is written in Rust. So it is automatically secure, right?
– Challenge Text
Original challenge files can be found here.
Setting the stage
We are given a simple web-application written in Rust using the Actix framework.
Looking at the server code we find a handler which allows us to retrieve the flag
if we are logged in as “almighty_administrator” with the “is_admin” key set to “of_course”:
fn hn_flag(req: &HttpRequest<AppState>) -> impl Responder {
let cookie = match load_cookie(req) {
Some(c) => c,
None => return redirect("/login/"),
};
if cookie.contains_key("username")
&& cookie["username"] == "almighty_administrator"
&& cookie.contains_key("is_admin")
&& cookie["is_admin"] == "of_course"
{
let body = FlagTemplate {
title: SITE_TITLE,
username: &cookie["username"],
flag: &req.state().flag, // <- This contains the flag
}
.render()
.unwrap();
HttpResponse::Ok().body(body)
} else {
HttpResponse::Forbidden()
.header(http::header::LOCATION, "/")
.finish()
}
}
Easy enough, let us just get one of these cookies.
So how do we login?
Looking then at the login handler we see that we cannot login as almighty anything
and we have laughably few privileges ("is_admin=lol no"):
fn hn_login_post(req: (Form<LoginParams>, HttpRequest<AppState>)) -> HttpResponse {
let (params, req) = req;
if params.username.contains("almighty") {
return redirect("/login/");
}
let mut cookie = HashMap::new();
cookie.insert("username".to_owned(), params.username.clone());
cookie.insert("is_admin".to_owned(), "lol no".to_owned());
let cookie = bake_cookie(&req, &cookie); // <- Can we unbake the cookie?
HttpResponse::Found()
.header(http::header::LOCATION, "/")
.cookie(http::Cookie::build("auth", cookie).path("/").finish())
.finish()
}
So we need to somehow forge a cookie ourselves with:
username=almighty_administrator&is_admin=of_course
We need to look at bake_cookie, which simply applies
a surely-super-legit authenticated encryption to the plaintext cookie
and base64 encodes the authenticated ciphertext:
fn bake_cookie(req: &HttpRequest<AppState>, map: &HashMap<String, String>) -> String {
let pt = urlencode(map);
let authenc = &req.state().authenc;
let mut buffer = vec![0; AuthEnc::ciphertext_size(pt.as_bytes())];
let ct = authenc.auth_encrypt(pt.as_bytes(), &mut buffer).unwrap();
base64::encode_config(ct, base64::URL_SAFE)
}
Next up: how to bake (and unbake) cookies.
Neither 3DES, nor HMAC
Delving into crypto.rs, we find that auth_encrypt functions as follows:
- Compute
tag = md5(k0 | pt) - Pad the plaintext with PKCS#7 padding:
ppt = pad-pkcs-5(tag | pt) - Encrypt 3 times in CBC mode:
ct = des-cbc(k3, des-cbc(k2, des-cbc(k1, ppt)))
- Output
ct
Clearly there are multiple problems here:
The message authentication code is not actually HMAC, but simply prefix hashing; which is vulnerable to a length extension attack on the Merkle-Damgård construction of MD5.
Due to the “mac-then-encrypt” construction employed, the code exposes a CBC padding oracle. A classical attack that arises since the padding must be removed before checking the message authentication code. Note also that it is not 3DES (Triple DES), but 3 times DES-CBC (if the IVs had predictable structure, you could crack each 56-bit key separately); another lie!
In the remainder of the post, I explore the constituent vulnerabilities in more detail and how to chain them to forge (almost) arbitrary messages. Overall our strategy will be as follows:
- Decrypt the cookie. Thereby obtaining the plaintext and the message authentication code.
- Extend cookie with: “
&username=almighty_administrator&is_admin=of_course”. - Reencrypt the cookie using the CBC-padding oracle.
- Set the forged cookie in a browser and retrieve the flag.
Where we apply the length extension attack in step 2.
Extending the cookie will be sufficient, since any repeated keys in the cookie will simply overwrite the previous value set by the previous key:
fn load_cookie(req: &HttpRequest<AppState>) -> Option<HashMap<String, String>> {
...
let decoded = urldecode(&pt);
let mut map = HashMap::new();
for (k, v) in decoded {
map.insert(k.to_string(), v.to_string());
}
Some(map)
}
Decrypting the cookie
In order to explain the attack on the unauthenticated 3DES-CBC encryption, let us start by visualising the triple application of CBC. Pictorially decryption of 6 blocks, yielding 3 blocks of plaintext looks as follows:
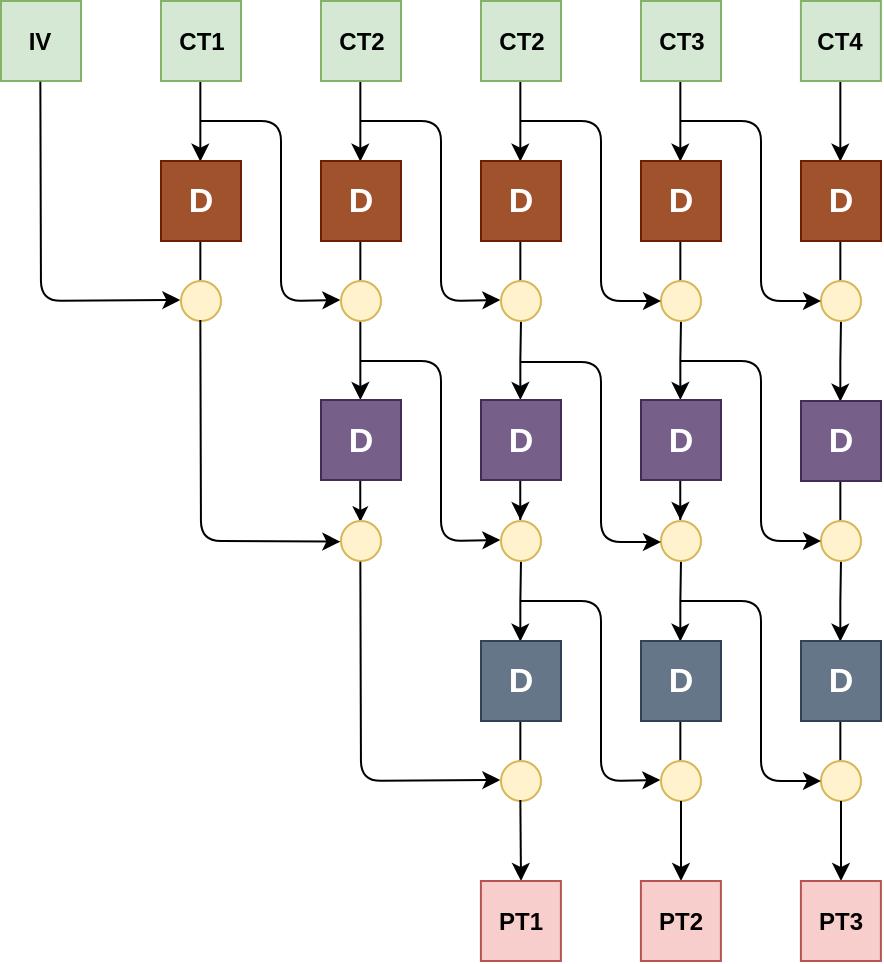
Where the yellow circles represent xor, and the “D” boxes are applications of the DES decryption function under different and (to us) unknown keys. There are 3 initialization vectors nested, one for each layer of encryption, hence the plaintext is only 3 blocks (\(\text{CT1}\) and \(\text{CT2}\) are encrypted IVs).
Now consider what happens if we modify the \(\text{IV}\) block by xoring a value \(\Delta\) into it: then the delta simply “propagates” down the left “stair” and \(\text{PT1}\) becomes \(\Delta \oplus \text{PT1}\). This means that, although we do not know the first block of plaintext, we can xor it with any value of our choosing.
Note that we can apply a similar trick with, e.g. \(\text{CT2}\) to control \(\text{PT3}\), however it will garble the first two blocks of the plaintext in an unpredictable way, since the delta is passed through the block cipher. This is illustrated below:
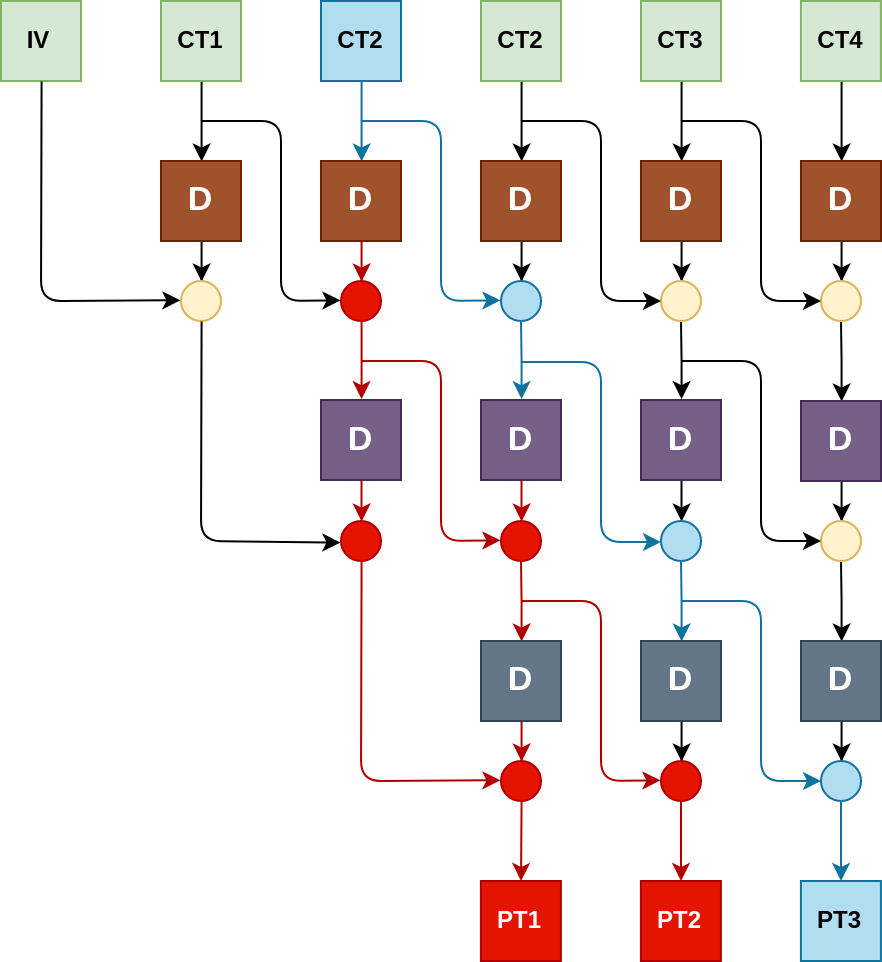
By xoring a \(\Delta\) into \(\text{CT2}\) all the blue values are xored with the same \(\Delta\). However these new values are passed through DES, which is, one would hope, highly non-linear and hence the red values are unknown and completely random to us. Note that this “garbling effect” only travels “backwards” during decryption, in other words: a hypothetical \(\text{PT4}\) would be unaffected in the example above; this will be relevant later when we want to encrypt.
Now lets talk about padding.
Since CBC only operates on messages which are a multiple of the block length, some sort of padding is needed. The padding employed here is PKCS#7 padding, where a message is padded to a multiple of the block size by appending bytes with a value equal to the number of padding required. If a message is already a multiple of the block size, then a full block of padding is added e.g. for a 64-bit block cipher (like DES):
pad-pkcs7("") -becomes-> "\x08\x08\x08\x08\x08\x08\x08\x08"
pad-pkcs7("A") -becomes-> "A\x07\x07\x07\x07\x07\x07\x07"
pad-pkcs7("HELLO") -becomes-> "HELLO\x03\x03\x03"
pad-pkcs7("HELLO AU") -becomes-> "HELLO AU\x08\x08\x08\x08\x08\x08\x08\x08"
After decryption, the server checks this padding, then removes the padding bytes as determined by inspecting the last byte of the plaintext. If the padding is invalid, the server will close the connection, otherwise it returns a HTML document.
The ability to check this “padding predicate” over the plaintext, coupled with the ability to modify the plaintext as observed before, will allow us to recover the full plaintext: We start by splitting the ciphertext (encrypted cookie), into overlapping 4 block (32 byte) chunks. e.g. in the case above, the 3 chunks would be:
\[ \text{IV} \ \ |\!| \ \ \text{CT1} \ \ |\!| \ \ \text{CT2} \ \ |\!| \ \ \text{CT2} \] \[ \text{CT1} \ \ |\!| \ \ \text{CT2} \ \ |\!| \ \ \text{CT2} \ \ |\!| \ \ \text{CT3} \] \[ \text{CT2} \ \ |\!| \ \ \text{CT2} \ \ |\!| \ \ \text{CT3} \ \ |\!| \ \ \text{CT4} \]
Then we decrypt each such chunk of the ciphertext individually, each of which will yield one block of plaintext: observe that when fed to the server the first block of the ciphertext chunk will be treated as the IV, by modifying this IV we change the plaintext block of the chunk as explained earlier. To see how we go about doing this, consider the last byte of the plaintext:
When we feed the server the chunk it reports “invalid padding”,
we then try xoring all possible values \(\Delta\) into the last byte of the IV (256 possibilities),
which cycles through all possible values of the last byte for the plaintext.
Eventually the server will return “valid padding”,
since a single \x01 byte at the end of the message is valid.
At this point we know that \(\Delta_7 \oplus \text{P1}_7 = 1\),
hence the last byte of the plaintext \(\text{P1}_7\) is \(\Delta_7 \oplus 1\) and
since we know delta (we chose it), we have recovered the last byte of the plaintext.
Since we now know the last byte of the plaintext,
we can make its value anything by modifying the IV.
The trick is to set the known part of the plaintext equal to a truncated padding sequence,
in the case of the last byte we make it \x02
and then we begin xoring the second byte of the IV until the server returns “valid padding”,
at which point we know that \(\text{P1}_6 = \Delta_6 \oplus 2\).
After recovering the second byte, we set it equal to \x03 and continue analogously for the remaining 6 bytes.
Note: There is an annoying case of false positives when recovering the last byte \(\text{P1}_7\),
since the message might happen to end with valid padding sequence for a longer padding than
a single byte, e.g. if the plaintext is “AAAA\x02\x02\x02W”,
then changing W into either 2 and 1 will yield valid padding.
This source of error can be eliminated by xoring any value into the second to last byte of the IV
after the server reports “valid padding”
and checking if the server still returns “valid padding”,
if not you have a false positive.
I use my simple CBC-padding oracle library to facilitate this part of the exploit.
Extending the message
So now we have the plaintext, most of which we already knew from the source code…
What we did gain was the message authentication code, recall that it was constructed as follows:
\[ mac = \text{MD5}(key \ |\!| \ msg) \]
The issue here, is that MD5 is a Merkle-Damgård construction: inside MD5 the message is processed in blocks, by applying a so-called compression-function, which takes:
- The current state of the hash (128-bit for MD5)
- A new block of data (512-bit for MD5)
And returns the new state of the hash (128-bit). I stole this illustration from wikipedia myself:
In the case of MD5 (unlike e.g. the Blake functions), there is no “finalization function” as described above. This means that if we know the hash digest, we can continue applying the compression function with new data!
The only thing we need to do is ensure that the data we append, include the length padding added to the original hash. Over simplifying a bit, this essentially means that we can can compute a valid \(mac’\): \[ mac' = f(mac, padding \ |\!| \ expend) = \text{MD5}(key \ |\!| \ msg \ |\!| \ padding \ |\!| \ extend) \] On the message \(msg \ |\!| \ padding \ |\!| \ extend\), where \(padding\) is the length padding of the original message and \(extend\) is any message of our desire.
We use HashPump to facilitate this part of the exploit.
Encrypting the cookie
So now we have a cookie with a valid MAC consisting of:
MAC [16 bytes]
+ username=lol&is_admin=lol no
+ A BUNCH OF LENGTH PADDING
+ &username=almighty_administrator&is_admin=of_course
But the server expects an encrypted cookie! Luckily it is easy to turn a CBC-decryption oracle (provided by our exploit + the CBC padding oracle), into an CBC-encryption oracle:
- We start by picking a random chunk (again 4 blocks, 32 bytes) of data: \[ ct = B_4 \ \ |\!| \ \ B_3 \ \ |\!| \ \ B_2 \ \ |\!| \ \ B_1 \]
- We decrypt the chunk using the oracle, yielding a random-looking plaintext \(pt_r\).
- We then change \(pt\) into the last block of our plaintext cookie \(pt_d\) by setting: \[ B_4 = B_4 \oplus pt_d \oplus pt_r \]
- We now prepend a new random block \(B_5\) to \(ct\) and repeat the procedure (from step 2) for the chunk \( B_5 \ \ |\!| \ \ B_4 \ \ |\!| \ \ B_3 \ \ |\!| \ \ B_2 \) and the second to last block of our cookie.
This works because of our previous observation about the garbling only propagating “backwards”; eventually it will “end up in the IVs”.
Putting it all together
With all the components now assembled, we put it together and wait…
My CBC padding oracle library can be found here \ Exploit for this challenge found here